bradipao.net
coding for fun whatever can be coded
Project maintained by bradipao Hosted on GitHub Pages — Theme by mattgraham
3D Koch Fractal
Basics on Koch curve
Koch curve is a mono-dimensional fractal that can be made tri-dimensional with an approach similar to the one followed for Sierpinski fractal. Koch curve is called also snowflake fractal because of its shape.
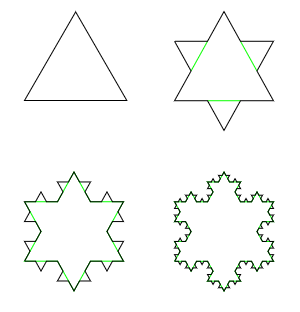
This fractal is said mono-dimensional because it is composed solely by lines, even if placed in a bi-dimensional space. The (obviously recursive) procedure to generate a Koch curve is simple:
- For each segment in the space:
- Divide segment in three equal sub-segments
- Replace the central sub-segment with two sub-segments, identical to removed one, placed as a triangle
- Repeat step 1 until number of iterations reached
The final result, at different numbers of iteratios, is shown in the figure below (from Wikipedia).
Koch 2D with openSCAD
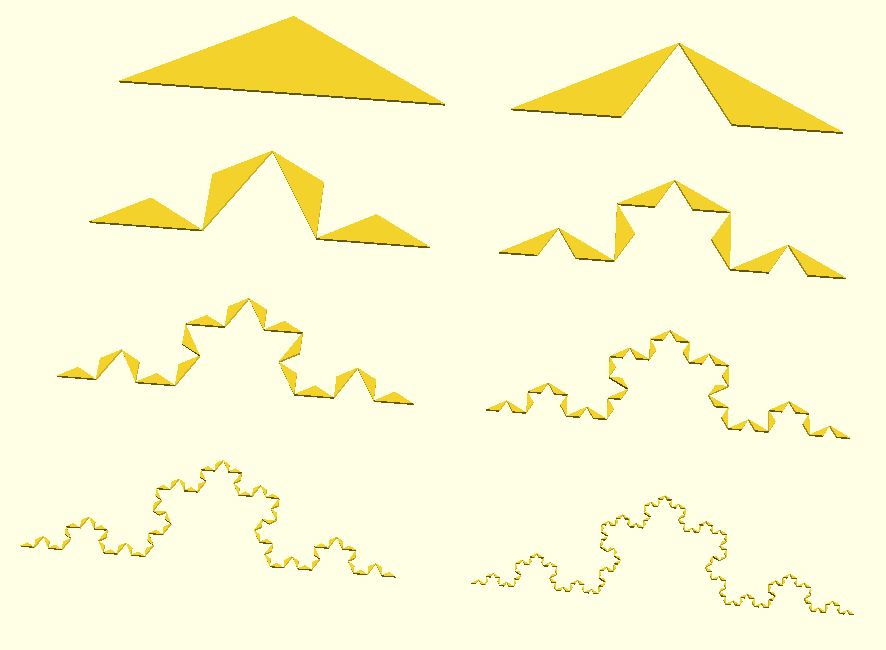
Before to face the tri-dimensional version, it is worth to make an intermediate step first and generate the bi-dimensional one. Before to proceed it is necessary to explain a fundamental property of fractals: the starting shape is not relevant for the final result, because with an infinite number of iterarions, shape itself is reduced to points of infinitely small size. The shape of a fractal is basically contained only in the geometric transformations, whichever the shape used at start. In our case, in order not to have to iterate infinitely, we wisely choose a shape that match the final shape given by the geometric transformation.
So, for the bi-dimensional version, we replace the starting mono-dimensional segment with an isosceles triangle, that is the envelope of the structure after the first step of above figure. We change also the recursive procedure, that now replaces a single isosceles triangle with two isosceles triangles, each with the base on one of the oblique sides of the original triangle and internal to the original triangle itself.
The key of these transformations is that the replacing triangles are fully contained in the original triangle and original perimeter is exactly preserved, even if a portion is left void. Increasing iterations of this procedure you will see that starting shape is every step less visibile, while overall shape is every step more similar to the ideal Koch curve. As stated above, shape is in the geometric transformation, not in starting shape.
Koch 3D with openSCAD
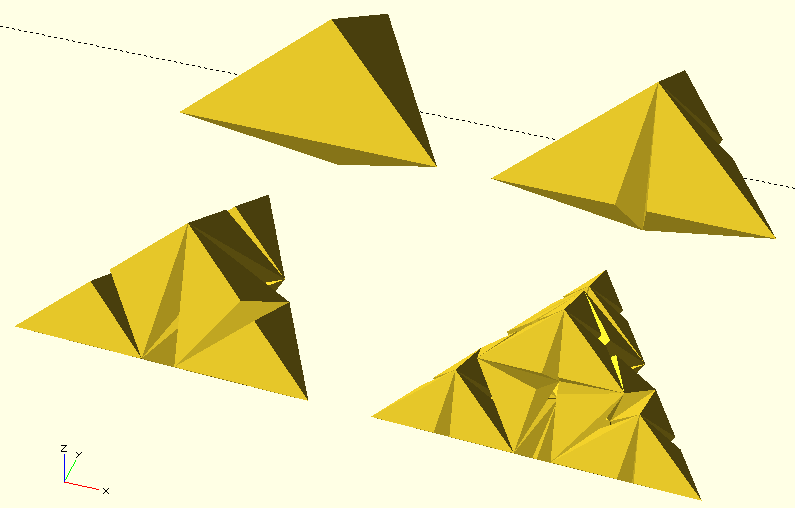
The tri-dimensional version is much less intuitive than the Sierpinski one, mostly because we cannot use a tetrahedron as starting shape (you will understand better once you see the final shape). The most suitable starting shape is composed by two isosceles tetrahedrons coupled on their basis and with a precise ration between side of base and height (let’s call it a double-tetrahedron). Our goal is to start from a shape that perfectly match the final shape of fractal, so that we obtain excellent result also with a few iterations.
As for the bi-dimensional version, we wnat to replace each double-tetrahedron with three smaller double-tetrahedrons, which preserve the original perimeter of the shape, but with some voids (like in the bi-dimensional one). The following figure shows the first iterations, hopefully to graphically explain above statement.
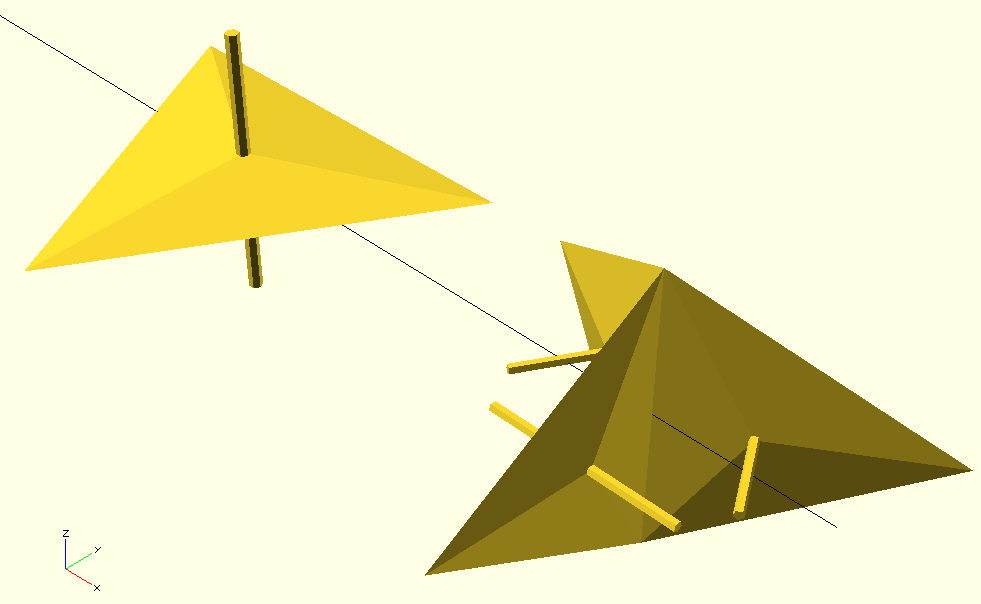
In next figure the double-tetrahedrons are replaced with just base and height (without oblique faces) in order to better show the geometric transformations.
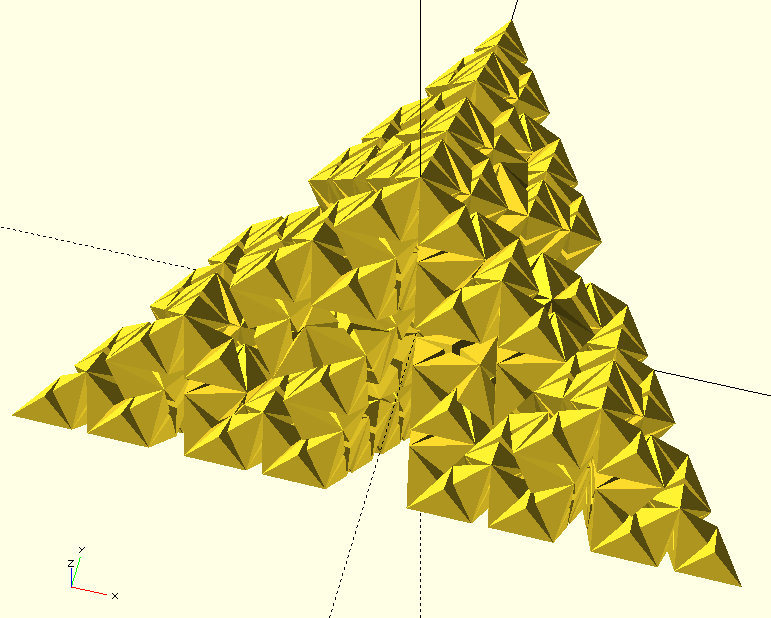
Next figure is the tri-dimensional version of Koch curve after 6 iterations. Again you can see that, even at this stage, the starting shape is barely detectable and the overall shape is something different, coming only from geometric transformations.
Show me the code
translate([0,-200,0]) koch2D(100,1,1);
translate([120,-200,0]) koch2D(100,1,2);
translate([0,-250,0]) koch2D(100,1,3);
translate([120,-250,0]) koch2D(100,1,4);
translate([0,-300,0]) koch2D(100,1,5);
translate([120,-300,0]) koch2D(100,1,6);
translate([0,-350,0]) koch2D(100,1,7);
translate([120,-350,0]) koch2D(100,1,8);
translate([-360,0,0]) koch3D(100,1,1);
translate([-240,0,0]) koch3D(100,1,2);
translate([-360,-120,0]) koch3D(100,1,3);
translate([-240,-120,0]) koch3D(100,1,4);
koch3D(100,1,6);
translate([200,0,0]) rotate([0,0,180]) koch3D_structure(100,1,1);
translate([320,0,0]) rotate([0,0,180]) koch3D_structure(100,1,2);
// koch 3D fractal
module koch3D(ww,nn,mm) {
if (nn<mm) {
rotate([0,0,120])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D(ww*2/3,nn+1,mm);
rotate([0,0,-120])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D(ww*2/3,nn+1,mm);
rotate([0,0,0])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D(ww*2/3,nn+1,mm);
} else {
tetrion(ww);
}
}
// double pyramid
module tetrion(ww) {
pp = [[-ww/2,-ww/(2*sqrt(3)),0],
[ww/2,-ww/(2*sqrt(3)),0],
[0,ww*(sqrt(3)/2 - 1/(2*sqrt(3))),0],
[0,0,ww/3],
[0,0,-ww/3]];
ff = [[3,1,0],
[3,2,1],
[3,0,2],
[0,1,4],
[1,2,4],
[2,0,4]];
polyhedron(pp,ff);
}
// koch 3D fractal structure
module koch3D_structure(ww,nn,mm) {
if (nn<mm) {
rotate([0,0,120])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D_structure(ww*2/3,nn+1,mm);
rotate([0,0,-120])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D_structure(ww*2/3,nn+1,mm);
rotate([0,0,0])
rotate([0,90,0])
translate([0,ww/(2*sqrt(3)*3/2),0])
koch3D_structure(ww*2/3,nn+1,mm);
} else {
tetrion_structure(ww);
}
}
// double pyramid structure
module tetrion_structure(ww) {
pp = [[-ww/2,-ww/(2*sqrt(3)),0],
[ww/2,-ww/(2*sqrt(3)),0],
[0,ww*(sqrt(3)/2 - 1/(2*sqrt(3))),0],
[0,0,ww/30],
[0,0,-ww/30]];
ff = [[3,1,0],
[3,2,1],
[3,0,2],
[0,1,4],
[1,2,4],
[2,0,4]];
polyhedron(pp,ff);
translate([0,0,-ww/3]) cylinder(d=ww/30,h=2*ww/3);
}
// koch 2D fractal
module koch2D(ww,nn,mm) {
if (nn<mm) {
translate([((ww/sqrt(3))*(sqrt(3)/2-1/sqrt(3))),0,0])
rotate([0,0,150])
translate([0,-ww/(3*2),0])
koch2D(ww/sqrt(3),nn+1,mm);
translate([-((ww/sqrt(3))*(sqrt(3)/2-1/sqrt(3))),0,0])
rotate([0,0,-150])
translate([0,-ww/(3*2),0])
koch2D(ww/sqrt(3),nn+1,mm);
} else {
tria(ww);
}
}
// triangle
module tria(ww) {
pp = [[-ww/2,0],[ww/2,0],[0,ww/(2*sqrt(3))]];
polygon(pp);
}