bradipao.net
coding for fun whatever can be coded
Project maintained by bradipao Hosted on GitHub Pages — Theme by mattgraham
3D Sierpinski Fractal
Basics on Sierpinski triangle
Among the peculiarities of openSCAD there is the support to recursion applied to 3D drawing. It is something I experienced when I was a kid messing with LOGO, actually I was too young to understand the abstraction of recursion concept, but I remember I found easy and powerful to define a basic graphic behavior and to repeat it in different positions with different scale and orientation. Today, after university studies and many personal experiments, I found quite natural to draw a Sierpinski fractal in openSCAD using recursion.
The “manual” procedure is quite simple:
- Draw one equilateral triangle on the sheet
- Replace any equilateral triangle on the sheet with three equilateral triangles, with side half size of original one, each placed in a vertex
- Repeat step 2 until number of iteration reached
Step 2 is the key of fractal generation, because at each iteration new details are added. Step 3 allows to repeat previous step for a predefined number of iterations, ideally an infinite one, but in practice limited to a very small number (definetely less than 10), because the computational effort grows exponentially with it.
The image below, taken from Wikipedia, show four iterations of the above procedure.

Sierpinski 2D with openSCAD
It is easy to implement the above procedure in openSCAD, with a few small tips that make code simpler and more effective.
Let’s start recalling the two basic characteristics which a recursive function must have:
- A way to call itself (the actual recursion)
- A condition to stop iterations (else function will call itself indefinitely)
If you take the first two iterations of the figure above, you understand that “the way to call itself” means literally repeating three time the function call to itself, but after moving in one of the three vertexes (translate() in openSCAD) and halving the size (we need a parameter to propagate size of triangle through iterations). The “condition to stop iteration” is managed passing other two parameters to the function, the first represents the current iteration cycle, the secondo is the maximum iteration cycle. When current cycle is equal to maximum cycle, instead of calling itself, triangle is drawn.
The result of this openSCAD code is the following:
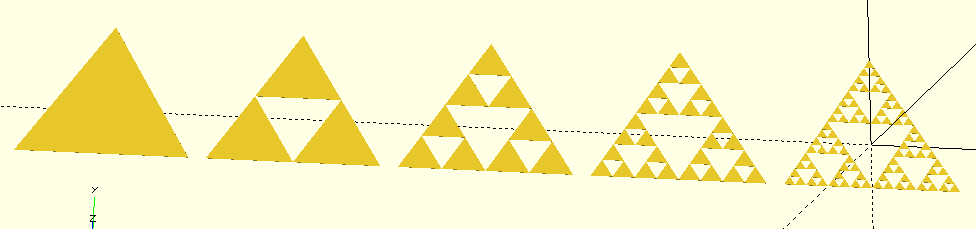
Sierpinski 3D
Once understood the basic concept, it is easy to extend it to third dimension and create a Sierpinski Tetrahedron. In place of the basic shape of a triangle, there is a tetrahedron and in place of the three half-sized triangles placed on the three vertexes of bigger triangle, there are four half-sized tetrahedrons placed in the four vertexes of the bigger tetrahedron.
Apart from the different spatial placement of geometric shapes, the structure of code is the same, and the result is the following:
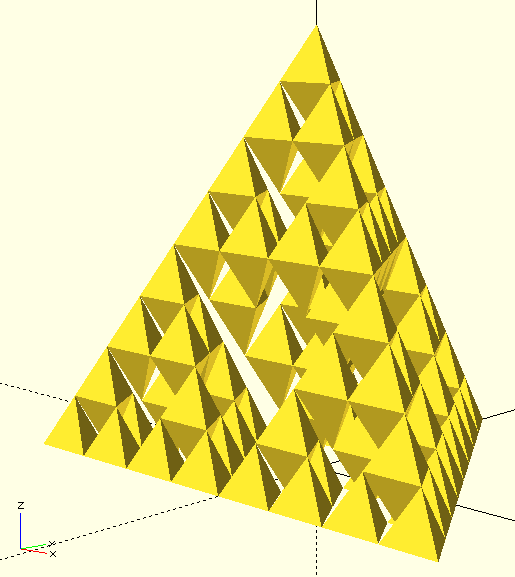
Rotating the tetrahedron in the space you can see that a fifth tetrahedron could be added inside the structure, a variation of the classical Sierpinski structure, but also much easier to 3D-print.
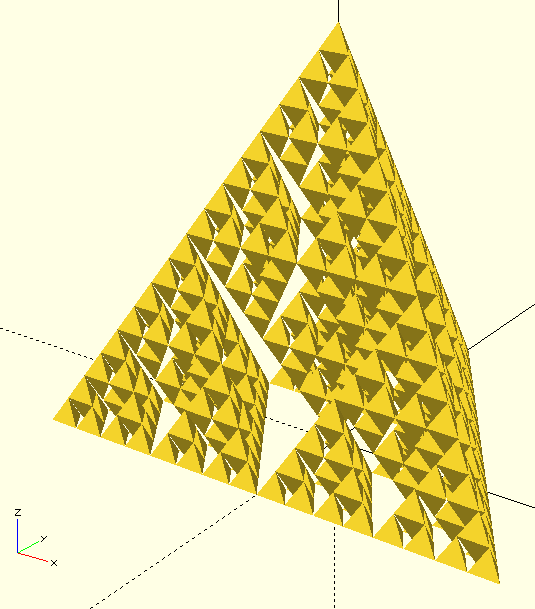
Recursion allows also to play with colors, for example assigning to end-of-iterations tetrahedrons a cumulative tone of red, blue or green every time a specific branch of iteration is chosen. The result is quite interesting:
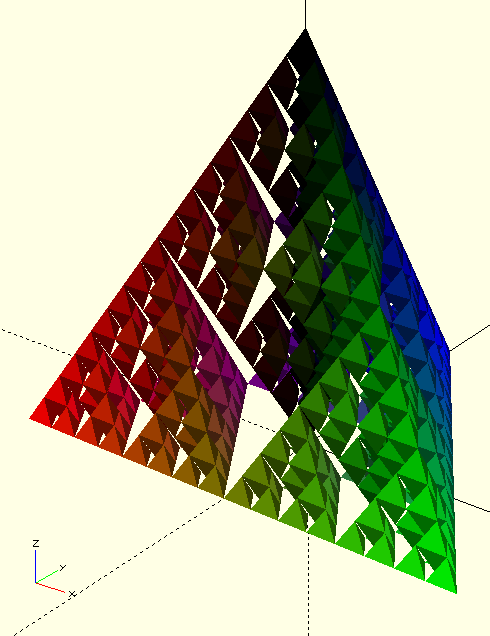
Show me the code
// example of COLORED SIERPISNKI 3D
sierpinski3Dc(200,1,5,0,0,0);
// tridimensional recursive sierpinski function
module sierpinski3Dc(ww,nn,mm,rr,gg,bb) {
// condition to propagate recursion
if (nn<mm) {
// single iteration of fractal transformation and recursion step
translate([-ww/4,-ww/8,0]) sierpinski3Dc(ww/2,nn+1,mm,rr+1/pow(2,nn),gg,bb);
translate([+ww/4,-ww/8,0]) sierpinski3Dc(ww/2,nn+1,mm,rr,gg+1/pow(2,nn),bb);
translate([0,ww/4,0]) sierpinski3Dc(ww/2,nn+1,mm,rr,gg,bb+1/pow(2,nn));
translate([0,0,ww/sqrt(6)]) sierpinski3Dc(ww/2,nn+1,mm,rr,gg,bb);
translate([0,0,ww/sqrt(6)]) mirror([0,0,1]) sierpinski3Dc(ww/2,nn+1,mm,rr,gg,bb);
}
// end of recursion, draw basic shape
else {
color([rr,gg,bb]) tetra(ww);
}
}
// example of SIERPISNKI 3D
translate([300,-500,0]) sierpinski3D(200,1,4);
// tridimensional recursive sierpinski function
module sierpinski3D(ww,nn,mm) {
// condition to propagate recursion
if (nn<mm) {
// single iteration of fractal transformation and recursion step
translate([-ww/4,-ww/8,0]) sierpinski3D(ww/2,nn+1,mm);
translate([+ww/4,-ww/8,0]) sierpinski3D(ww/2,nn+1,mm);
translate([0,ww/4,0]) sierpinski3D(ww/2,nn+1,mm);
translate([0,0,ww/sqrt(6)]) sierpinski3D(ww/2,nn+1,mm);
//color("Brown") translate([0,0,ww/sqrt(6)]) mirror([0,0,1]) tetrion(ww/2);
translate([0,0,ww/sqrt(6)]) mirror([0,0,1]) sierpinski3D(ww/2,nn+1,mm);
}
// end of recursion, draw basic shape
else {
tetra(ww);
}
}
module tetra(ww) {
pp = [[-ww/2,-ww/4,0],
[ww/2,-ww/4,0],
[0,ww/2,0],
[0,0,ww*sqrt(6)/3]];
ff = [[0,1,2],
[0,1,3],
[1,2,3],
[2,0,3]];
polyhedron(pp,ff);
}
// example of SIERPISNKI 2D
translate([0,-500,0]) union() {
translate([ 0,0,0]) sierpinski2D(200,1,5);
translate([-220,0,0]) sierpinski2D(200,1,4);
translate([-440,0,0]) sierpinski2D(200,1,3);
translate([-660,0,0]) sierpinski2D(200,1,2);
translate([-880,0,0]) sierpinski2D(200,1,1);
}
// bidimensional recursive sierpinski function
module sierpinski2D(ww,nn,mm) {
// condition to propagate recursion
if (nn<mm) {
// single iteration of fractal transformation and recursion step
translate([-ww/4,-ww/8,0]) sierpinski2D(ww/2,nn+1,mm);
translate([+ww/4,-ww/8,0]) sierpinski2D(ww/2,nn+1,mm);
translate([0,ww/4,0]) sierpinski2D(ww/2,nn+1,mm);
}
// end of recursion, draw basic shape
else {
tria(ww);
}
}
// basic shape : triangle
module tria(ww) {
pp = [[-ww/2,-ww/4],[ww/2,-ww/4],[0,ww/2]];
polygon(pp);
}
// tretrahedron for 3d printing
module tetrion2(ww) {
wi = ww*1.1;
pp = [[-wi/2,-wi/4,0],[wi/2,-wi/4,0],[0,wi/2,0],[0,0,wi*sqrt(6)/3]];
ff = [[0,2,1],[0,1,3],[1,2,3],[2,0,3]];
polyhedron(pp,ff);
}